PRABI-Doua: baobabLuna

baobabLUNA: the solution space of sorting by reversals

The package baobabLUNA is a java framework to deal with permutations that represent genomes in rearrangement analysis. baobabLUNA contains a collection of classes for building breakpoint graphs (the basic structures behind the work on genome rearrangements), performing reversals, calculating reversal distances, sorting permutations. Includes a text representation for the breakpoint graph (class baobab.bio.permutation.PermutationBPGraphFormatter).

baobabLUNA is only able to deal with unichromosomal genomes and its main functionality is the implementation of an algorithm that gives a compact representation of the space of all solutions of the sorting by reversals problem, that is, a representation of all optimal sequences of reversals that sort one genome into another.

A reduced on-line documentation of baobabLUNA (with some interface aspects and tutorial of executable programs) is offered in this website (see bellow). A full documentation (with complete methodological background, technical aspects, interface description, download & setup instructions and tutorial of executable programs) is provided in PDF format here. We also provide download of compiled code and java API.

Developed by Marília D. V. Braga.

Preliminary version - last update November 2008.

Full documentation in PDF format: complete methodological background, technical aspects, interface description, download & setup instructions and tutorial of executable programs.
On-line documentation
2.1. Interface aspects: the text representation for the breakpoint graph
2.2. List of programs and tutorial

A list of programs which deal with permutations
A program to generate a representation of the space of all solutions for the sorting by reversals problem (and the modified versions, which filter solutions using constraints)
Examples (tutorial)

Download (Compiled code & Java API)
References

2. On-line documentation

2.1. Interface aspects: the text representation for the breakpoint graph

The breakpoint graph is represented by a string with four lines. The first, the second and the third lines represent the cycles' black and gray edges (... represents an adjacency). The fourth line contains the given origin permutation.

Example: for the linear permutation -4,-3,12,-11,-8,10,9,7,-6,-5,2,-1, we have the following text representation of its breakpoint graph:

  01. 02. 03. 04. 05. 06. 07. 08. 09. 10. 11. 12. 13.              [A]
  01> ... 01> <01 03> <02 <03 <02 02> ... 01> <01 <01              [B]
  :11 ... :04 :13 :07 :09 :05 :06 :08 ... :12 :03 :01              [C]
:: -04 -03 +12 -11 -08 +10 +09 +07 -06 -05 +02 -01  :: 5 cycles    [D]

[A] Black edges' index line: the black edges are numbered in increasing order.

[B] Black edges' direction: each black edge receives a direction, according to an arbitrary tour in the corresponding cycle (each cycle receives a unique arbitrary number, thus two edges with the same numbers are in the same cycle).

[C] Gray edges: each cycle tour in the direction induced by black edges' direction (the number after the ":" indicates the next black edge to be visited, referring to the [first] index line).

[D] Permutation line: the given permutation and the number of cycles (adjacencies + long cycles) in the corresponding breakpoint graph.

The graphical representation of this breakpoint graph follows (the unique arbitrary number of each long cycle is indicated):

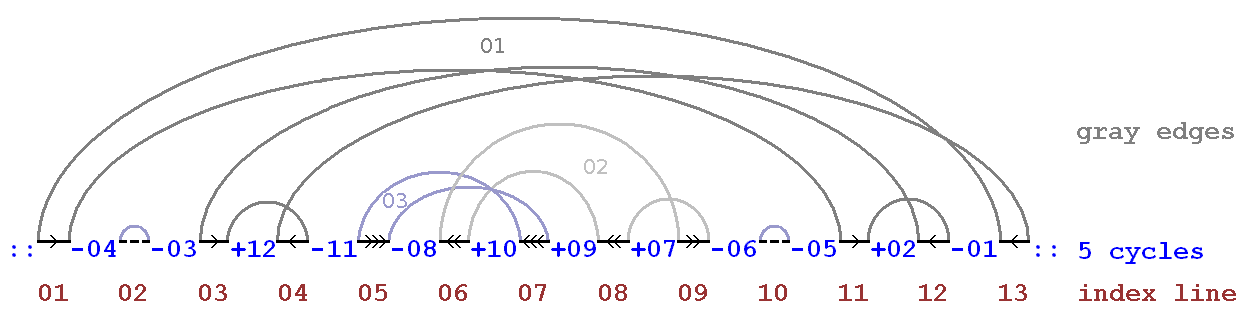
The text representation of breakpoint graphs is largely used in our executable programs. It is implemented by the class baobab.bio.permutation.PermutationBPGraphFormatter (consult the class API to get a description of its usability).

2.2. List of executable programs and tutorial

2.2.1. A list of programs which deal with permutations

2.2.2. A program to generate a representation of the space of all solutions for the sorting by reversals problem (and the modified versions, which filter solutions using constraints)

2.2.3. Examples (tutorial)

2.2.1. A list of programs which deal with permutations

package baobab.exec.permutation

analyzeSignedPermutation: analyzes a signed permutation and prints its breakpoint graph and reversal distance
analyzeUnsignedPermutation: analyzes an unsigned permutation and prints its breakpoint graph
collapsePermutation: collapses a breakpoint graph of a signed permutation to eliminate its adjacencies
decomposeSignedPermutation: decomposes a breakpoint graph of a signed permutation into its components
getComplexFirstReversals: finds all optimal reversals for the given signed permutation (this program deals with hurdles, but does not deal with a fortress)
getFirstOrientedReversals: finds all optimal reversals for the given signed permutation (this program does not deal with hurdles)
performReversals: perform the reversals (defined by their beginning and end points) in the given order
sort: sorts the given signed permutation (this program deals with hurdles, but does not deal with a fortress)

2.2.2. A program to generate a representation of the space of all solutions for the sorting by reversals problem (and the modified versions, which filter solutions using constraints)

package baobab.exec.trace

analyzeTraces: Analyzes the space of all solutions for the sorting by reversals problem for the given signed permutation - a trace represents a class of solutions. This program enumerates all traces without enumerating all solutions, and counts the number of solutions represented by each trace. It returns the list of traces represented by their normal forms and the respective number of solutions in each trace (this program does not deal with hurdles). The algorithm is described in [4],[5].

Attention: the number of traces may be huge for permutations with reversal distance greater than 12. During its execution, the program has to keep a considerable amount of data, but its intern organization allows automatic partial and required global compression of this data (there are parameters to set the level of compression).

Applying biological constraints When biological constraints are applied, the program analyzes the space of all sorting sequences that respect the given constraints only. It returns the list of non-empty traces that are in agreement with the constraints.

Analyzing the traces whose solutions do not break the initially detected common intervals between the two given permutations (perfect traces): the parameter -p -1 may be given. The version of this program that accepts common interval breaks is not implemented in baobabLUNA.
Analyzing the traces whose solutions do not break the progressively detected common intervals between the two given permutations (progressive perfect subtraces), accepting at most i>=0 common interval breaks: the parameter -p i may be given.
Analyzing the strata-induced subtraces of a permutation: the permutation must be linear, the first stratum is assumed to start in point 1, then each stratum starts in the end point of the previous stratum. The strata end points may be given by the following parameter: -s [points] (points may be separated by commas, without spaces). Example: -s 7,15,23. This version is described in [5].

To get the help, run the program without arguments.

2.2.3. Examples (tutorial)

Getting help
Sorting a linear signed permutation
Sorting a circular signed permutation
Calculating the reversal distance of a linear signed permutation
Performing reversals on a linear signed permutation
Analyzing the traces of a linear signed permutation (1)
Analyzing the traces of a linear signed permutation (2)
Analyzing the traces whose solutions do not break the initially detected common intervals of a linear signed permutation (perfect traces)
Analyzing the traces whose solutions do not break the progressively detected common intervals of a linear signed permutation (progressive perfect subtraces)
Analyzing the strata-induced subtraces of a linear signed permutation

Example - Getting help:

>java -classpath baobab-luna.jar baobab.exec.permutation.sort

Sorts the given signed permutation (this program does not deal with hurdles)

Required parameters:

   -o originPermutation (values separated by commas, without spaces)
        Ex: -o -4,-3,12,-11,-8,10,9,7,-6,-5,2,-1

Optional parameters:

   -t targetPermutation (values separated by commas, without spaces)
        Ex: -t 5,-3,12,10,9,8,-11,7,-6,-4,2,-1

   -l T/F (T=linear [default], F=circular)
        Ex: -l F

Example - Sorting the linear permutation -3 +2 +1 -4:

>java -classpath baobab-luna.jar baobab.exec.permutation.sort -o -3,2,1,-4

  1. 2. 3. 4. 5.
  1> <1 1> <1 1>
  :5 :3 :1 :2 :4
:: -3 +2 +1 -4  :: 1 cycles

Reversal distance: 4

Solution:

  1. 2. 3. 4. 5.
  1> <1 1> <1 1>
  :5 :3 :1 :2 :4
:: -3 +2 +1 -4  :: 1 cycles
   ---             (from [1] -3 to -3 [2])
  1. 2. 3. 4. 5.
  2> <1 2> <1 1>
  :3 :5 :1 :2 :4
:: +3 +2 +1 -4  :: 2 cycles
      ---------    (from [2] +2 to -4 [5])
  1. 2. 3. 4. 5.
  2> .. 1> <2 1>
  :4 .. :5 :1 :3
:: +3 +4 -1 -2  :: 3 cycles
   ---------       (from [1] +3 to -1 [4])
  1. 2. 3. 4. 5.
  .. <1 .. .. 1>
  .. :5 .. .. :2
:: +1 -4 -3 -2  :: 4 cycles
      ---------    (from [2] -4 to -2 [5])
  1. 2. 3. 4. 5.
  .. .. .. .. ..
  .. .. .. .. ..
:: +1 +2 +3 +4  :: 5 cycles

Example - Sorting the circular permutation -3 +2 +1 -4 (observe that the circular permutations -3 +2 +1 -4 and -1 -2 +3 +4 are equivalent):

>java -classpath baobab-luna.jar baobab.exec.permutation.sort -l F -o -3,2,1,-4

  1. 2. 3. 4.
  1> <1 1> ..
  :3 :1 :2 ..
:: -1 -2 +3 +4  :: 2 cycles

Reversal distance: 2

Solution:

  1. 2. 3. 4.
  1> <1 1> ..
  :3 :1 :2 ..
:: -1 -2 +3 +4  :: 2 cycles
   ---          (from [1] -1 to -1 [2])
  1. 2. 3. 4.
  .. <1 1> ..
  .. :3 :2 ..
:: +1 -2 +3 +4  :: 3 cycles
      ---       (from [2] -2 to -2 [3])
  1. 2. 3. 4.
  .. .. .. ..
  .. .. .. ..
:: +1 +2 +3 +4  :: 4 cycles

Example - Calculating the reversal distance of the permutation +23 +22 +1 +4 +7 +10 +9 +8 +11 +6 +5 +12 +15 +18 +17 +16 +19 +14 +13 +20 +3 +2 +21 (a fortress - 12 cycles, 6 unoriented components, no oriented components, 3 super-hurdles, no simple-hurdles):

>java -classpath baobab-luna.jar baobab.exec.permutation.analyzeSignedPermutation -o 23,22,1,4,7,10,9,8,11,6,5,12,15,18,17,16,19,14,13,20,3,2,21

  01. 02. 03. 04. 05. 06. 07. 08. 09. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24.
  01> 12> 01> 02> 04> 06> 07> 06> 07> 05> 04> 05> 08> 10> 11> 10> 11> 09> 08> 09> 03> 02> 03> 12>
  :03 :24 :01 :22 :11 :08 :09 :06 :07 :12 :05 :10 :19 :16 :17 :14 :15 :20 :13 :18 :23 :04 :21 :02
:: +23 +22 +01 +04 +07 +10 +09 +08 +11 +06 +05 +12 +15 +18 +17 +16 +19 +14 +13 +20 +03 +02 +21  :: 12 cycles

Reversal distance: 16

Example - Performing reversals on the permutation -4 -3 +12 -11 -8 +10 +9 +7 -6 -5 +2 -1:

>java -classpath baobab-luna.jar baobab.exec.permutation.performReversals -o -4,-3,12,-11,-8,10,9,7,-6,-5,2,-1 -r "11,13|3,13"

  01. 02. 03. 04. 05. 06. 07. 08. 09. 10. 11. 12. 13.
  01> ... 01> <01 03> <02 <03 <02 02> ... 01> <01 <01
  :11 ... :04 :13 :07 :09 :05 :06 :08 ... :12 :03 :01
:: -04 -03 +12 -11 -08 +10 +09 +07 -06 -05 +02 -01  :: 5 cycles

Reversal distance: 8

Reversals:

  01. 02. 03. 04. 05. 06. 07. 08. 09. 10. 11. 12. 13.
  01> ... 01> <01 03> <02 <03 <02 02> ... 01> <01 <01
  :11 ... :04 :13 :07 :09 :05 :06 :08 ... :12 :03 :01
:: -04 -03 +12 -11 -08 +10 +09 +07 -06 -05 +02 -01  :: 5 cycles
                                           --------     (from [11] +02 to -01 [13])
  01. 02. 03. 04. 05. 06. 07. 08. 09. 10. 11. 12. 13.
  04> ... 01> <01 03> <02 <03 <02 02> ... 04> 01> <01
  :11 ... :04 :13 :07 :09 :05 :06 :08 ... :01 :03 :12
:: -04 -03 +12 -11 -08 +10 +09 +07 -06 -05 +01 -02  :: 6 cycles
           ----------------------------------------     (from [03] +12 to -02 [13])
  01. 02. 03. 04. 05. 06. 07. 08. 09. 10. 11. 12. 13.
  04> ... 05> <05 <04 ... <02 02> 03> 02> <03 01> <01
  :05 ... :04 :03 :01 ... :08 :10 :11 :07 :09 :13 :12
:: -04 -03 +02 -01 +05 +06 -07 -09 -10 +08 +11 -12  :: 7 cycles

Example - Analyzing the traces of the permutation -3 +2 +1 -4:

>java -classpath baobab-luna.jar baobab.exec.trace.analyzeTraces -o -3,2,1,-4

  1. 2. 3. 4. 5.
  1> <1 1> <1 1>
  :5 :3 :1 :2 :4
:: -3 +2 +1 -4  :: 1 cycles

summary:

Reversal distance: 4

Total number of 4-traces: 2
Total number of solutions: 28

Distribution by height:
Height=1: 1 traces; 24 solutions
Height=3: 1 traces; 4 solutions

Distribution by width:
Width=2: 1 traces
Width=4: 1 traces

The first biggest trace follows:
{1}{1.-.3}{2}{4} : h=1 [24]

4-traces:

{1}{1.-.3}{2}{4} : h=1 [24] w=4
{1.2.4}{3} < {1.3.4} < {2.-.4} : h=3 [4] w=2

Number of 4-traces: 2
Solutions computed by 4-traces: 28

Example - Analyzing the traces of the permutation -4 -3 +12 -11 -8 +10 +9 +7 -6 -5 +2 -1:

>java -classpath baobab-luna.jar baobab.exec.trace.analyzeTraces -o -4,-3,12,-11,-8,10,9,7,-6,-5,2,-1

  01. 02. 03. 04. 05. 06. 07. 08. 09. 10. 11. 12. 13.
  01> ... 01> <01 03> <02 <03 <02 02> ... 01> <01 <01
  :11 ... :04 :13 :07 :09 :05 :06 :08 ... :12 :03 :01
:: -04 -03 +12 -11 -08 +10 +09 +07 -06 -05 +02 -01  :: 5 cycles

summary

Reversal distance: 8

Total number of 8-traces: 6
Total number of solutions: 31752

Distribution by height:
Height=2: 3 traces; 30240 solutions
Height=4: 3 traces; 1512 solutions

Distribution by width:
Width=4: 3 traces
Width=6: 3 traces

The first biggest trace follows:
{1.2}{1.2.5.-.12}{2}{7}{8.10}{12} < {1.-.4}{8.9} : h=2 [10080]

8-traces

{1.2}{1.2.5.-.12}{2}{7}{8.10}{12} < {1.-.4}{8.9} : h=2 [10080] w=6
{1.-.12}{2}{3.4.12}{5.-.11}{7}{8.10} < {3.-.11}{8.9} : h=2 [10080] w=6
{1.-.12}{2.-.12}{2.5.-.12}{7}{8.10}{12} < {2.-.4}{8.9} : h=2 [10080] w=6
{1.2}{7}{8.10} < {1.5.-.11}{8.9} < {1.3.4.12} < {2.-.12}{3.-.11} : h=4 [336] w=4
{2.-.12}{7}{8.10} < {1.3.4.12}{8.9} < {1.5.-.11} < {1.2}{3.-.11} : h=4 [336] w=4
{2.5.-.12}{5.-.11}{7}{8.10} < {1.12}{8.9} < {1.5.-.11} < {1.-.4} : h=4 [840] w=4

Number of 8-traces: 6
Solutions computed by 8-traces: 31752

Example - Analyzing the perfect traces of the permutation -5,-2,-7,4,-8,3,6,-1: (perfect traces are those whose solutions do not break the initially detected common intervals of a permutation)

>java -classpath baobab-luna.jar baobab.exec.trace.analyzeTraces -p -1 -o -5,-2,-7,4,-8,3,6,-1

1. 2. 3. 4. 5. 6. 7. 8. 9.
  1> <1 1> <1 1> 1> <1 1> <1
  :7 :5 :6 :8 :9 :2 :4 :3 :1
:: -5 -2 -7 +4 -8 +3 +6 -1  :: 1 cycles

summary:

Reversal distance: 8

8-traces:

{1.-.8}{2}{2.-.5.7.8}{2.4.7} < {2.3.7.8}{2.8} < {2.-.6}{7.8} : [1288]
{1.-.8}{2}{2.-.5.7.8}{2.4.7}{3.8} < {2.4.-.7}{4.-.6} < {3.-.7} : [2072]
...
{1.-.8}{2.4.7.8} < {2.-.4.6.7} < {2.3.5.-.8} < {2.-.6.8} < {4.5.7.8} < {4.6.7} < {5.-.7} : [8]
{1.-.8}{3.4.6.8} < {2.6.7} < {2.-.4.8} < {4.6.7} < {3.6.-.8} < {3.-.5.8} < {3.-.7} : [8]

Total number of 8-traces: 92
Total number of solutions: 51304

Example - Analyzing the progressive perfect subtraces of the permutation -5,-2,-7,4,-8,3,6,-1: (progressive perfect subtraces are those whose solutions do not break the progressively detected common intervals of a permutation)

>java -classpath baobab-luna.jar baobab.exec.trace.analyzeTraces -p 0 -o -5,-2,-7,4,-8,3,6,-1

1. 2. 3. 4. 5. 6. 7. 8. 9.
  1> <1 1> <1 1> 1> <1 1> <1
  :7 :5 :6 :8 :9 :2 :4 :3 :1
:: -5 -2 -7 +4 -8 +3 +6 -1  :: 1 cycles

summary:

Reversal distance: 8

8-traces:

{1.-.8}{2}{2.-.5.7.8}{2.4.-.7}{3.8}{2.4.7}{4.-.6}{3.-.7} (representative)
{1.-.8}{2}{2.-.5.7.8}{2.4.7}{3.8} < {2.4.-.7}{4.-.6} < {3.-.7} (normal form)
[112] (size)

{1.-.8}{2}{2.-.5.7.8}{3.8}{4}{3.4.7}{2.-.4}{2.-.6} (representative)
{1.-.8}{2}{2.-.5.7.8}{3.8}{4} < {3.4.7} < {2.-.4}{2.-.6} (normal form)
[1344] (size)

...

{1.-.8}{2.-.5.7.8}{2.4.-.7}{2.3.5.-.8}{2.-.6.8}{3.4.7.8}{3.-.7}{5.-.7} (representative)
{1.-.8}{2.-.5.7.8} < {2.4.-.7} < {2.3.5.-.8} < {2.-.6.8} < {3.4.7.8} < {3.-.7}{5.-.7} (normal form)
[16] (size)

Total number of 8-subtraces: 12
Total number of solutions: 11568

Example - Analyzing the strata-induced subtraces of the permutation -4 -3 +12 -11 -8 +10 +9 +7 -6 -5 +2 -1, with the strata end points at positions (points) 03., 11. and 13.:

>java -classpath baobab-luna.jar baobab.exec.trace.analyzeTraces -s 3,11,13 -o -4,-3,12,-11,-8,10,9,7,-6,-5,2,-1

  01. 02. 03. 04. 05. 06. 07. 08. 09. 10. 11. 12. 13.
  01> ... 01> <01 03> <02 <03 <02 02> ... 01> <01 <01
  :11 ... :04 :13 :07 :09 :05 :06 :08 ... :12 :03 :01
:: -04 -03 +12 -11 -08 +10 +09 +07 -06 -05 +02 -01  :: 5 cycles

summary

Reversal distance: 8

Strata end points:
> 3 (between -3 and 12)
> 11 (between -5 and 2)
> 13 (after -1)

Total number of 8-traces: 1
Total number of solutions: 420

Distribution by height:
Height=2: 1 traces; 420 solutions

Distribution by width:
Width=6: 1 trace

The first biggest trace follows:
{1.2}{1.2.5.-.12}{2}{7}{8.10}{12} < {1.-.4}{8.9} : h=2 [420]

8-traces

{1.2}{1.2.5.-.12}{2}{7}{8.10}{12} < {1.-.4}{8.9} : h=2 [420] w=6

Number of 8-traces: 1
Solutions computed by 8-traces: 420

3. Download

Here you can download the full compiled code (including executables) and the API documentation with the list of classes and functionalities of the package baobab.bio.permutation only.

Version 1.1 beta (21/Nov/2008)

Executable, lib (jar) >> baobab-luna.jar
Documentation (API) >> baobab-luna-api.tar.gz

Version 1.0 beta (28/Apr/2008)

Executable, lib (jar) >> baobab-luna-1.0beta.jar
Documentation (API) >> baobab-luna-api-1.0beta.tar.gz

Version 0.4 beta (01/Aug/2007)

Executable, lib (jar) >> baobab-luna-0.4beta.jar
Documentation (API) >> baobab-luna-api-0.4beta.tar.gz

Version 0.3 beta (02/Mar/2007)

Executable, lib (jar) >> baobab-luna-0.3beta.jar
Documentation (API) >> baobab-luna-api-0.3beta.tar.gz

Version 0.2 beta (22/Nov/2006)

Executable, lib (jar) >> baobab-luna-0.2beta.jar
Documentation (API) >> baobab-luna-api-0.2beta.tar.gz

Version 0.1 beta (15/Nov/2006)

Executable, lib (jar) >> baobab-luna-0.1beta.jar
Documentation (API) >> baobab-luna-api-0.1beta.tar.gz

4. References

Braga M. D. V., Gautier C. and Sagot M-F., An asymmetric approach to preserve common intervals while sorting by reversals, Algorithms for Molecular Biology, 2009.
Braga M. D. V., babobabLUNA: the solution space of sorting by reversals, Bioinformatics, vol. 25, no. 14, 1833--1835, 2009.
Braga M. D. V., Exploring the solution space of sorting by reversals when analyzing genome rearrangements. PhD thesis, 2009. Available here.
Braga M. D. V, Sagot M.-F., Scornavacca C. and Tannier E., Exploring The Solution Space of Sorting by Reversals With Experiments and an Application to Evolution, Transactions on Computational Biology and Bioinformatics, vol. 5, no. 3, 348--356, 2008.

Braga M. D. V, Sagot M.-F., Scornavacca C. and Tannier E., The Solution Space of Sorting by Reversals, ISBRA 2007, Lecture Notes in Bioinformatics 4463, 293-304, 2007.

Bergeron A., Chauve C., Hartmann T., St-Onge K., On the properties of sequences of reversals that sort a signed permutation. JOBIM 2002, 99-108.

Hannenhalli, S. and Pevzner, P. A. Transforming cabagge into turnip (polynomial algorithm for sorting signed permutations by reversals). In Proceedings of the 27th Annual ACM-SIAM Symposium on the Theory of Computing, pages 178-189, 1995.

Hannenhalli, S. and Pevzner, P. A. Transforming men into mice (polynomial algorithm for genomic distance problem). In Proceedings of the IEEE 36th Annual Symposium on Foundations of Computer Science, pages 581-592, 1995.

Java

Developed by Marília D. V. Braga

Preliminary version - last update November 2008